pyzag.chunktime

Functions and objects to help with blocked/chunked time integration.

These include:

Sparse matrix classes for banded systems
General sparse matrix classes
Specialized solver routines working with banded systems

class pyzag.chunktime.BidiagonalForwardOperator(*args, inverse_operator=<class 'pyzag.chunktime.BidiagonalThomasFactorization'>, **kwargs)

A batched block banded matrix of the form:

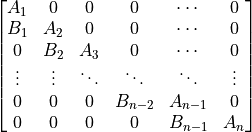
$\begin{bmatrix} A_1 & 0 & 0 & 0 & \cdots & 0\\ B_1 & A_2 & 0 & 0 & \cdots & 0\\ 0 & B_2 & A_3 & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & B_{n-2} & A_{n-1} & 0\\ 0 & 0 & 0 & 0 & B_{n-1} & A_n \end{bmatrix}$

that is, a blocked banded system with the main diagonal and first lower block diagonal filled

We use the following sizes:

nblk: number of blocks in the square matrix
sblk: size of each block
sbat: batch size

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) storing the nblk diagonal blocks
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) storing the nblk-1 off diagonal blocks

forward(v)

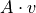$A \cdot v$ in an efficient manner

Parameters:: v (torch.tensor) – batch of vectors

inverse(): Return an inverse operator

matvec(v)

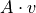$A \cdot v$ in an efficient manner

Parameters:: v (torch.tensor) – batch of vectors

to_diag(): Convert to a SquareBatchedBlockDiagonalMatrix, for testing or legacy purposes

vecmat(v)

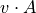$v \cdot A$ in an efficient manner

Parameters:: v (torch.tensor) – batch of vectors

pyzag.chunktime.BidiagonalHybridFactorization(min_size=1): Apply the hybrid factorization with a given min_size

class pyzag.chunktime.BidiagonalHybridFactorizationImpl(*args, min_size=0, **kwargs)

A factorization approach that switches from PCR to Thomas

Specifically, this class uses PCR until the PCR chunk size is smaller than user provided minimum chunk size. Then it switches to Thomas.

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) with the main diagonal
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) with the off diagonal

Keyword Arguments:

min_size (int) – minimum block size, default is zero

matvec(v)

Complete the backsolve for a given right hand side

Parameters:: v (torch.tensor) – tensor of shape (nblk, sbat, sblk, 1)

class pyzag.chunktime.BidiagonalOperator(A, B, *args, **kwargs)

An object working with a Batched block diagonal operator of the type

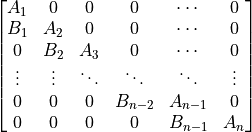
$\begin{bmatrix} A_1 & 0 & 0 & 0 & \cdots & 0\\ B_1 & A_2 & 0 & 0 & \cdots & 0\\ 0 & B_2 & A_3 & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & B_{n-2} & A_{n-1} & 0\\ 0 & 0 & 0 & 0 & B_{n-1} & A_n \end{bmatrix}$

that is, a blocked banded system with the main diagonal and the first lower diagonal filled

We use the following sizes:

nblk: number of blocks in the square matrix
sblk: size of each block
sbat: batch size

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) storing the nblk main diagonal blocks
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) storing the nblk-1 off diagonal blocks

property device: device, which is just the device of self.diag

property dtype: dtype, which is just the dtype of self.diag

property n: Size of the unbatched square matrix

property shape: Logical shape of the dense array

class pyzag.chunktime.BidiagonalPCRFactorization(*args, **kwargs)

Manages the data needed to solve our bidiagonal system via parallel cyclic reduction

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) with the main diagonal
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) with the off diagonal

matvec(v)

Complete the backsolve for a given right hand side

Parameters:: v (torch.tensor) – tensor of shape (nblk, sbat, sblk)

class pyzag.chunktime.BidiagonalThomasFactorization(*args, **kwargs)

Manages the data needed to solve our bidiagonal system via Thomas factorization

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) with the main diagonal
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) with the off diagonal

matvec(v)

Complete the backsolve for a given right hand side

Parameters:: v (torch.tensor) – tensor of shape (nblk, sbat, sblk)

class pyzag.chunktime.ChunkNewtonRaphson(rtol=1e-06, atol=1e-10, miter=200, throw_on_fail=False, record_failed=False, ignore_batches=None)

Solve a nonlinear system with Newton’s method where the residual and Jacobian are presented as chunked operators

Keyword Arguments:

rtol (float) – nonlinear relative tolerance
atol (float) – nonlinear absolute tolerance
miter (int) – maximum number of iterations
throw_on_fail (bool) – if True, throw an exception on a failed solve. If False just issue a warning.
record_failed (bool) – if True, store the indices of the bad batches
ignore_batches (list of indices) – if provided, don’t check these batches in evaluating the stopping criteria

not_converged(nR, nR0)

The logical to determine if we’ve converged in a particular time/batch

Parameters:

nR (torch.tensor) – current residual
nR0 (torch.tensor) – original residual

setup(x): Do any initialization required before solving

solve(fn, x0)

Actually solve the system

Parameters:

fn (function) – function that returns the residual and Jacobian (as appropriate chunked operators)
x0 (torch.tensor) – initial guess, again properly chunked

Returns:

solution

Return type:

torch.tensor

step(x, J, fn, R0, take_step)

Take a simple Newton step

Parameters:

x (torch.tensor) – current solution
dx (torch.tensor) – newton increment
fn (function) – function
R0 (torch.tensor) – current residual
take_step (torch.tensor) – which entries to take a step with

class pyzag.chunktime.ChunkNewtonRaphsonLineSearch(*args, alpha=0.5, linesearch_iter=3, **kwargs)

Newton Raphson with backtracking line search

Keyword Arguments:

rtol (float) – nonlinear relative tolerance
atol (float) – nonlinear absolute tolerance
miter (int) – maximum number of iterations
throw_on_fail (bool) – if True, throw an exception on a failed solve. If False just issue a warning.
record_failed (bool) – if True, store the indices of the bad batches
ignore_batches (list of indices) – if provided, don’t check these batches in evaluating the stopping criteria
alpha (float) – line search cutback
linesearch_iter (int) – maximum number of line search iterations

step(x, J, fn, R0, take_step)

Take a Newton step with backtracking line search

Parameters:

x (torch.tensor) – current solution
dx (torch.tensor) – newton increment
fn (function) – function
R0 (torch.tensor) – current residual
take_step (torch.tensor) – which entries to take a step with

class pyzag.chunktime.LUFactorization(*args, **kwargs)

A factorization that uses the LU decomposition of A

Parameters:

A (torch.tensor) – tensor of shape (nblk,sbat,sblk,sblk) with the main diagonal
B (torch.tensor) – tensor of shape (nblk-1,sbat,sblk,sblk) with the off diagonal

forward(v)

Run the solve using the linear algebra type interface with the number of blocks and block size squeezed

Parameters:: v (torch.tensor) – tensor of shape (sbat, sblk*nblk)

class pyzag.chunktime.SquareBatchedBlockDiagonalMatrix(data, diags)

A batched block diagonal matrix of the type

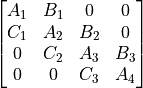
$\begin{bmatrix} A_1 & B_1 & 0 & 0\\ C_1 & A_2 & B_2 & 0 \\ 0 & C_2 & A_3 & B_3\\ 0 & 0 & C_3 & A_4 \end{bmatrix}$

where the matrix has diagonal blocks of non-zeros and can have arbitrary numbers of filled diagonals

Additionally, this matrix is batched.

We use the following sizes:

nblk: number of blocks in the each direction
sblk: size of each block
sbat: batch size

Parameters:

data (list of tensors) – list of tensors of length ndiag. Each tensor has shape (nblk-abs(d),sbat,sblk,sblk) where d is the diagonal number provided in the next input
diags (list of ints) – list of ints of length ndiag. Each entry gives the diagonal for the data in the corresponding tensor. These values d can range from -(n-1) to (n-1)

property device: device, as reported by the first entry in self.device

property dtype: dtype, as reported by the first entry in self.data

property n: Size of the unbatched square matrix

property nnz: Number of logical non-zeros (not counting the batch dimension)

property shape: Logical shape of the dense array

to_batched_coo()

Convert to a torch sparse batched COO tensor

This is done in a weird way. torch recognizes “batch” dimensions at the start of the tensor and “dense” dimensions at the end (with “sparse” dimensions in between). batch dimensions can/do have difference indices, dense dimensions all share the same indices. We have the latter situation so this is setup as a tensor with no “batch” dimensions, 2 “sparse” dimensions, and 1 “dense” dimension. So it will be the transpose of the shape of the to_dense function.

to_dense(): Convert the representation to a dense tensor

to_unrolled_csr(): Return a list of CSR tensors with length equal to the batch size

pyzag.chunktime.thomas_solve(lu, pivots, B, v)

Simple function implementing a Thomas solve

Solves in place of v

Parameters:

lu (torch.tensor) – factorized diagonal blocks, (nblk,sbat,sblk,sblk)
pivots (torch.tensor) – pivots for factorization
B (torch.tensor) – lower diagonal blocks (nblk-1,sbat,sblk,sblk)
v (torch.tensor) – right hand side (nblk,sbat,sblk)