Phase-Field Fracture

Table of Contents

• Crack geometric functions
• Degradation functions
• Strain Energy Density
• Example

The phase-field fracture physics module is a collection of objects serving as building blocks for composing models describing the evolution of regularized fracture, and the accompanying loss of materials' load-bearing capacity. The models defined in this module offer a set of phase-field fracture constitutive choices that can be utilized to set up a fracture simulation using both staggered and monolithic solution schemes.

This module can be coupled with other physics modules to describe energy dissipation coupled with fracture. For example, the solid mechanics module can be coupled to simulate a variety of (visco)plastic dissipation. This documentation offers a short description of each object under this module followed by a comprehensive example showing how each of them can be used to compose a bigger model describing fracture evolution locally at independent material points.

Crack geometric functions

The crack geometric function, \( \alpha(\phi) \) determines the distribution of the crack phase field that governs the "shape" of the smeared crack. Given the phase field, \( \phi \), it calculates the corresponding scalar-valued crack geometric function. Below are some example crack geometric functions.

• CrackGeometricFunctionAT1
• CrackGeometricFunctionAT2

Degradation functions

Generally, as the fracture evolves, the material gradually loses its load-carrying capacity. Given the phase field, \( \phi \), the degradation function, \( g(\phi) \) calculates the corresponding scalar-valued function to degrade the materials' stiffness. Some example degradation functions are listed below.

• PowerDegradationFunction
• RationalDegradationFunction

Strain Energy Density

This module also offers definitions of the strain energy density to facilitate the setup of variational constitutive update. Given the strain as input, the strain energy density objects calculate the active part of the strain energy density, \( \psi_\mathrm{active} \) that drives the fracture propagation and the inactive part, \( \psi_\mathrm{inactive} \).

Example

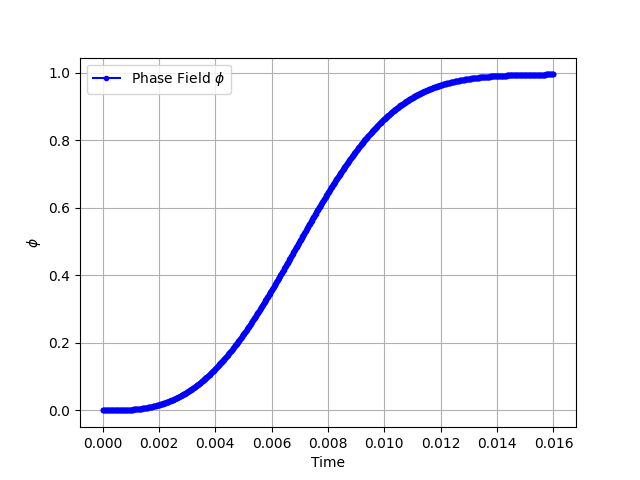
In this section, we'll describe how everything discussed above fits together to compose a bigger model that can be used to simulate fracture evolution at material points. Consider the following governing equation for crack propagation

\begin{align} f & = \eta \dot{\phi} + \frac{\partial}{\partial \phi} \left( \alpha \frac{G_c}{c_0 l} + g(\phi) \psi_\mathrm{active} \right) \ge 0, \quad \dot{\phi} \ge 0, \quad f \dot{\phi} = 0, \end{align}

which can be equivalently formulated using the Fischer-Burmeister complementarity condition as

\begin{align} f + \dot{\phi} - \sqrt{ f^2 + \dot{\phi}^2 } = 0. \end{align}

The complementarity condition can be implicitly solved for the phase field, \( \phi \) using the ImplicitUpdate model. The implicit equation can also be coupled with other physics. The following example input file walks through the model composition where \( d \) is used instead of \( \phi \) as the phase-field variable for the sake of brevity.

## Applying KKT conditions with the help of Fisher-Burmeister complementary condition
 
[Drivers]
  [driver]
    type = TransientDriver
    model = 'model'
    prescribed_time = 'times'
    force_SR2_names = 'E'
    force_SR2_values = 'strains'
    save_as = 'result.pt'
  []
  [regression]
    type = TransientRegression
    driver = 'driver'
    reference = 'gold/result.pt'
  []
[]
 
[Tensors]
  [times]
    type = LinspaceScalar
    start = 0
    end = 3
    nstep = 1000
  []
  [exx]
    type = FullScalar
    value = 0.016
  []
  [eyy]
    type = FullScalar
    value = -0.008
  []
  [ezz]
    type = FullScalar
    value = -0.008
  []
  [max_strain]
    type = FillSR2
    values = 'exx eyy ezz'
  []
  [strains]
    type = LinspaceSR2
    start = 0
    end = max_strain
    nstep = 1000
  []
  [p]
    type = Scalar
    values = 2
  []
  [GcbylbyCo]
    type = Scalar
    values = 0.0152 # Gc/l/Co with Gc = 95 N/m, l = 3.125 mm, Co = 2
  []
[]
 
[Models]
  # strain energy density: g * psie0
  [degrade]
    type = PowerDegradationFunction
    phase = 'd'
    degradation = 'g'
    power = 'p'
  []
  [sed0]
    type = LinearIsotropicStrainEnergyDensity
    strain = 'E'
    active_strain_energy_density = 'psie_active'
    inactive_strain_energy_density = 'psie_inactive'
    coefficient_types = 'YOUNGS_MODULUS POISSONS_RATIO'
    coefficients = '25.84e3 0.18'
    # decomposition = 'NONE'
    decomposition = 'VOLDEV'
  []
  [sed1]
    type = ScalarMultiplication
    from = 'g psie_active'
    to = 'psie_degraded'
  []
  [sed]
    type = ScalarLinearCombination
    from = 'psie_degraded psie_inactive'
    to = 'psie'
    weights = '1 1'
  []
  # crack geometric function: alpha
  [cracked]
    type = CrackGeometricFunctionAT2
    phase = 'd'
    crack = 'alpha'
  []
  # total energy
  [sum]
    type = ScalarLinearCombination
    from = 'alpha psie'
    to = 'psi'
    weights = 'GcbylbyCo 1'
  []
  # this guy maps from (strain, d) -> energy
  [energy]
    type = ComposedModel
    models = 'degrade sed0 sed1 sed cracked sum'
  []
  # phase rate, follows from variation of total energy w.r.t. phase field
  [dpsidd]
    type = Normality
    model = 'energy'
    function = 'psi'
    from = 'd'
    to = 'dpsi_dd'
  []
  # obtain d_rate
  [drate]
    type = ScalarVariableRate
    variable = 'd'
  []
  # define functional
  [functional]
    type = ScalarLinearCombination
    from = 'dpsi_dd d_rate'
    to = 'F'
    weights = '1 1'
  []
  # Fisher Burmeister Complementary Condition
  [Fish_Burm]
    type = FBComplementarity
    a = 'F'
    b = 'd_rate'
    complementarity = 'd_residual'
    a_inequality = 'LE'
  []
  # system of equations
  [eq]
    type = ComposedModel
    models = 'Fish_Burm functional drate dpsidd'
  []
[]
 
[EquationSystems]
  [eq_sys]
    type = NonlinearSystem
    model = 'eq'
    unknowns = 'd'
  []
[]
 
[Solvers]
  [newton]
    type = Newton
    rel_tol = 1e-08
    abs_tol = 1e-10
    max_its = 50
    linear_solver = 'lu'
  []
  [lu]
    type = DenseLU
  []
[]
 
[Models]
  # solve for d
  [predictor]
    type = LinearExtrapolationPredictor
    unknowns_Scalar = 'd'
  []
  [solve_d]
    type = ImplicitUpdate
    equation_system = 'eq_sys'
    solver = 'newton'
    predictor = 'predictor'
  []
  # after the solve take derivative of the total energy w.r.t. strain to get stress
  [stress]
    type = Normality
    model = 'energy'
    function = 'psi'
    from = 'E'
    to = 'S'
  []
  [model]
    type = ComposedModel
    models = 'solve_d stress'
    additional_outputs = 'd'
  []
[]

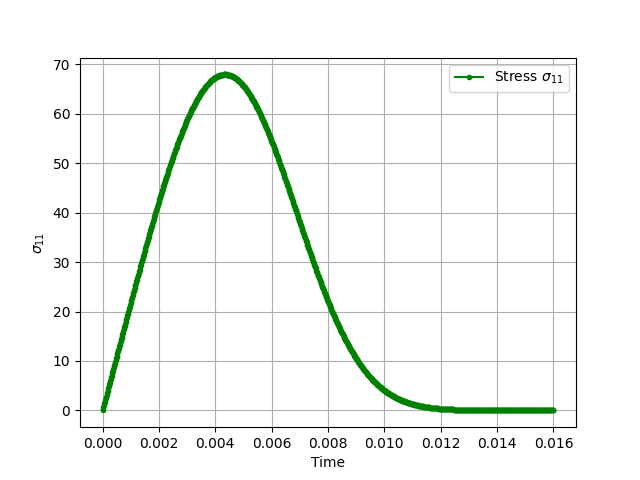
The stress evaluated at the end of the input file acts only as a post-processor to verify our results.